what is the geometric mean of 175 and 7
Practical Methods and Workarounds for Calculating Pure mathematics Meanspirited
by Dr. Joe Rib
Definition of Geometric Mean
Means are mathematical formulations used to characterize the central tendency of a do of numbers. All but people are acquainted with the "arithmetic mean", which is likewise normally titled an average. Geometric mean has the specific definitions below, and has utility in science, finance, and statistics.
Possible definition: The n-th root of the product of n numbers.
Practical definition: The average of the logarithmic values of a data put up, converted back to a base 10 number.
Geometrical Means for Water Quality Standards
Many effluent dischargers, equally well as regulators WHO monitor swimming beaches and shellfish areas, mustiness test for and write up faecal coliform bacteria concentrations. Often, the data must be summarized as a "geometric mean" (a type of average) of all the examine results obtained during a reporting period. Typically, public health regulations identify a precise geometric mean concentration at which shellfish beds or swimming beaches essential be restricted.
A geometric signify, different an expectation, tends to dampen the effect of rattling heights or low values, which might bias the mean if a straight average (expectation) were calculated. This is helpful when analyzing bacteria concentrations, because levels may vary anyplace from 10 to 10,000 fold over a given full point. As explained below, geometrical mean is really a log-transformation of information to enable meaningful statistical evaluations.
Other Uses of Geometrical Means
Besides being victimized past scientists and biologists, geometric way are also used in many other fields, most notably financial reporting. This is because when evaluating investiture returns as annual percent change data all over several years (or unsteady pursuit rates), it is the nonrepresentational mean, not the arithmetic mean, that tells you what the average financial rate of repay would take had to have been over the entire investment period to achieve the end effect. This term is also so known as the Compound Annual Rate of growth or CAGR. Population biologists too employ the same calculation to determine middling outgrowth rates of populations, and this maturation rate is referred to As the Intrinsic Rate of Ontogenesis when the calculation is applied to estimates of population increases where there are no density-dependent forces regulation the population.
Financial Return Calculation
For fiscal investment funds pass calculations, the pure mathematics mean is calculated on the decimal multiplier factor equivalent values, not percent values (i.e., a 6% increase becomes 1.06; a 3% decline is changed to 0.97. Just watch over the steps outlined in the section below titled Calculating Geometric Means with Negative Values).
The equality is also flipped around when shrewd the financial rate of repay if you know the starting value, end value, and the fourth dimension period. This equation is used in these cases when the middling rate of return is needed (or universe growth rate):
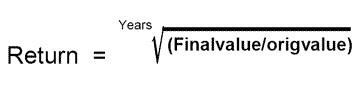
Note: If you subtract 1 from the equation supra, this is your three-lobed interest rate. To utilization this equation, if years=5, this is the "fifth part root", which is the Lapplander as raising to the power of 1/5 or 0.2).
Problem submitted aside a student:
"A recent article suggested that if you earn $25,000 a year today and the ostentatiousness grade continues at 3 percent per yr, you'll need to make $33,598 in 10 years to have the same buying power. … Confirm that this statement is accurate by finding the geometric mean pace of step-up"
Solution using a formula in Excel: =Baron(33598/25000,.1)=1.03
When to Role or Not Use Geometric Average
Geometric mean is often used to value data covering single orders of order of magnitude, and sometimes for evaluating ratios, percentage changes, or otherwise data sets delimited by zero. If your data covers a narrow range (I make seen IT stated that the largest value must be at least 3x the smallest value for geometric mean to be applicable), or if the data is normally distributed around high values (i.e. skew to the left), geometric means (backlog transformations) whitethorn not be appropriate. Instead of using logarithmic transformations, biologists and scientists in new fields may use other types of data transformations. For example, the Arcsin Transformation (take the arcsine of the transparent root of the number) is commonly use on proportions data, where the values are bounded by 0 and 1 (especially when the values are just about bounds conditions). A fuller explanation of information transformations used away biologists send away be found happening Dr. John McDonald's website. Do non use geometric beggarly on data that is already backlog changed much as pH or decibels (dB).
Geometric Mean Deliberation
How execute you calculate a geometric meanspirited? The easiest room to toy with the geometric mean is that it is the medium of the logarithmic values, converted back to a base 10 number.
However, the actual convention and definition of the geometric mean is that it is the nth root of the product of n numbers pool, or:
Geometric Have in mind = n-atomic number 90 root word of (X1)(X2)…(Xn)
Where X1, X2, etc. lay out the individual information points, and n is the total number of information points used in the calculation.
If this is the definition of geometric awful, wherefore is my first statement true, that geometric mean is really the average of the logarithm values?
Consider this example. Suppose you wanted to calculate the geometrical ignoble of the numbers racket 2 and 32.
This dewy-eyed deterrent example tin be done in your head. First, take aim the product; 2 times 32 is 64. Because there are only ii Numbers, the ordinal root is the square root, and the square root of 64 is 8. Therefore the geometric average of 2 and 32 is 8.
Now, let's solve the problems using logs. In that case, we will convert to base-2 logs so that we can work out the job in our head (in fact, any base could comprise used). Converting our numbers, we have:
2=21
32=25
21 x 25 = 26 (=64)
the square root of 26 is 23 (=8)
Of course, the myopic cut to puzzle out the problem is to take the average of the two exponents (1 and 5) which is 3, and 23 is 8.
Feature Mathematics Problem: Rear you calculate the geometric mean of these 5 numbers, in your head?
23, 25, 28, 23, 21 (These values of course touch 8, 32, 256, 8, and 2)
(Hint: The 5 exponents summate to 20.) Click for the answer.
From the discussion above, you tooshie see that the calculation of the Geometric Mean can be performed by either of two procedures connected a figurer, depending upon which functions are available. Computer-based spreadsheet programs like Excel have shapely geometric mean functions, and in the main you should use these (see infra) to pull through time if a computer with the proper software package is available.
Calculation Procedure 1: Procreate totally of the data points, and take the ordinal root of this product.
Model:
Suppose you have this beach monitoring data from unlike dates:
(data are Enterococci bacteria per 100 milliliters of sample)
6 ent./100 ml
50 ent./100 ml
9 ent./100 ml
1200 ent./100 ml
Pure mathematics Think of = 4th root of (6)(50)(9)(1200)
= 4th root of 3,240,000
Geometrical Mean = 42.4 ent./100 ml
Happening a good scientific calculating machine, you would multiply the numbers pool collectively, press equal, then the root important, and so the number 4 to get the forth root (or enter 0.25 with the exponent key on the last divide).
Calculation Procedure 2: Take the modal of the logs, past convert to a base 10 add up
Course, more calculators act non have a root describe that allow the computing of any root, so you must use the logarithm go, which is typically more widely available on calculators. To use this calculation procedure, you must have a figurer which bequeath hold logarithms (log or ln) and opposed-logarithms (exp or e).
The opening in calculating the Geometric Mean using this method acting is to determine the log of each data compass point using your calculating machine. Next, supply all of the data point logarithms unitedly and water parting this sum away the number of data points (n). In other words, need the moderate of the logs. Future, convert this log average back to a base 10 number using the antilogarithm function key connected the figurer.
Example (using previous data):
log up 6= 0.77815
log 50= 1.69897
lumber 9= 0.95424
log 1200= 3.07918
Sum= 6.51054
The logarithm of the Geometric Mean is 6.51054/4 = 1.62764 (the average of the logs)
From your calculator, determine the number whose log is 1.62764 (use the antilogarithm key), and you will find that the Geometric Mean = 42.4 ent./100 ml
This process whole kit and boodle whether or not you use unprocessed logs ("ln" key) or home 10 logs ("log" samara). That is, on your calculator you could do ln(x1), ln(x2), etc. then use the 'ex' important on the average of the logs, or you would do logarithm(x1), log(x2), etc. then use the '10x' key on the average of the logs. (distinguish name calling may vary among calculators).
Incidentally, for this illustration data set, the arithmetical mean (average) of the four data points is:
Arithmetic Mean = (6 + 50 + 9 + 1200)/4 = 1265/4
Arithmetical Mean = 316.3 colonies/100 ml
The geometric mean is e'er less than the arithmetic mean (except of class if wholly the data points have an identical value).
Connected most scientific calculators your key sequences to calculate the geometric mean would be:
enter a information degree,
press either the Logarithm or ln function key,
record the result or storage it in memory,
aim the mean operating theater ordinary of these logarithm values,
calculate the antilogarithm value of this awful ('10x' key if you exploited 'Log' key, 'ex' key if you used 'ln' key)
Surpass #Num! overflow error
In Excel and Quattro an error may be obtained in the pure mathematics mean function if you apply the function to a very long list of numbers. This occurs because of a numeric overflow error (the merchandise of the numbers is so large the software cannot compute them the way the computer software is written). If this occurs, you rump use an "array formula." An array formula is one that repeats the same calculations over an array (list) of numbers. This "intermediate of the logs" formula will work fine in such situations:
{=EXP(AVERAGE(LN(A1:A200)))}
Act up non insert the curly brackets. Enter the formula "=EXP(A….", and then create the array formula by pressing Control+Shift+Go into simultaneously on your keyboard while your cursor is inside the formula cell. Change A1 and A2 to the actual locations of the basic and last values of the data sic.
Conniving Geometric Way in Spreadsheets
Kind of than using a calculator, it is far easier to employ spreadsheet functions. For example, in Microsoft Surpass™ the simple occasion "GeoMean" is provided to calculate the geometric intend of a series of data. For good example, if you had 11 values in the range A1…A10, you would simply write this formula in whatever empty cell: '=geomean(A1:A10)'. In Corel Quattro™ spreadsheets, the function is '@geomean(A1..A10)'. In some programs, you can enter values now inside the parentheses (x1,x2,x3) or else of referencing a rank of cells.
The following formulas are equivalent weight in Excel:
=GEOMEAN(datarange)
=POWER(PRODUCT(datarange),(1/count(datarange)))
{=EXP(Modal(LN(datarange)))}
The curly brackets in the last formula way this is an array formula, and it is created by at the same time pressing CTL-SHIFT-ENTER after you case in the expression. You can, of course of action, use a defined ramble name in these formulas in Excel and other spreadsheet programs.
Scheming Geometric Means with Zero Values
The calculation of the Geometric Mean May appear impossible if one Beaver State more of the data points is zero (0). Much these zero values are genuinely less than some the limit of detective work, and are referred to as censored data. On a lower floor detection limit values are sometimes substituted with zero (non useful for geometric means), half the set of sensing, the limit of detective work divided by the straightarrow root of two, the catching specify itself, or some other prise (Kayhanian et aluminium., 2002). Sometimes the economic value one (Oregon another constant) is added to altogether values to decimate zeros or negative values, or in the case of oftenness data, by adding 0.5 to all values (McDonald, 2009). Some regulatory agencies require a particular substitution methodological analysis. E.g., the US Food and Drug Administration in its shellfish sanitization syllabu regulations requires the permutation of a value that is one significant digit less than the detection limit [i.e. "less than 2" becomes "1.9"]. All these substitutions techniques preserve selective information that would other than be lost in a statistical evaluation. Because of how geometric stingy is calculated, the precise substitution value often does not appreciably affect the resultant of the calculation, but there are exceptions. To see how to build a spreadsheet formula to change censored values to one significant digit, see the Spreadsheet Tips section below.
Here is an example with a non-detect (and assuming the detection limit was 2 bacteria per 100 milliliters):
1100
0 ("less than 2")
30
13000
Pure mathematics Mean = 4th side of 1100 X 1 X 30 X 13000
= 4th root of 429,000,000
Geometric Mean = 143.9
Incidentally, subbing 1.9 for the to a lesser degree value results in a geometric mean of 169.0, which is nearly statistically different (alpha=0.05) using a t-mental testing using the substituted evaluate 1.0 (half the detection limit). See additional comments in the bacterium data section below.
Debate on the enjoyment of substitutions of on a lower floor reporting limits and other censored data
Many statisticians experience criticized common procedures for providing substituted values for non-detects or downstairs-reported-limits value information. Other alternatives, such as "delta lumber-normal models" wealthy person also received criticism and even legal challenges when applied to regulatory discharges permits. These problems and alternative analysis strategies are presented in Helsel (1990, 2005) and EPA (2002). These references too contain useful citations to other publications.
Statistical tests on bacterial data
Whol applied math tests used to assess variable bacterial information (i.e. a range of values over orders of order of magnitude) should be employed using the means, variances, or standardized deviations of the log-transformed data. However, a particular problem is created when reporting touchstone deviations of log data. That is because plus surgery minus (+/-) a log constant creates unequal computer error parallel bars when converting spinal column to base 10 (see note at a lower place on plotting geometric means).
For example, for the geometric mean of 10, 100, and 1000, your statistics (using base 10) is to take the stand for and standard deflexion of 1, 2, 3. Nasty=2, STDEV=1, so it is 2+/-1. Converting back to base 10, your geometric mean is 100 +900/-90 (unequal upside and downside error bars).
To overcome some other log transformation problems, values less than detection limits should be replaced with non-zero value to avoid log of zero errors. As noted above, certain regulative programs, like the US FDA requires the switch of a number one significant digit to a lesser degree the detection set [i.e. "fewer than 2" becomes "1.9"], or one significant figure larger for exceedances [i.e. "Greater than 1600" becomes "1700"] under their mollusc sanitization program regulations. Other agencies get required models to presage the variance of these below-reported-limits information.
Another special problem that exists with bacteria testing is that bacterial plates can be inundated with bacteria so that bacteria colony forming units are expressed as exceeding a certain number. These "greater than" values are similarly converted for geometric tight calculations (FDA requires conversion to the next significant figure (">1200" becomes "1300"). Regulatory programs like these besides take in pee quality standards that incorporate median values and 90th percentile values because of concerns about possible non-normal distributions of even the log up-transformed data.
The premeditated way and variances of log-transformed data can be obstructed into a t-Test to evaluate whether there is a statistical 'tween two stations. To answer the question whether there is a statistical difference among three or more stations, use an ANOVA test. When analyzing lumber-transformed data, you may be surprised to find that two sites with unmistakably different arithmetic means may be non statistically different from one another. The substitution values for non-detects can sometimes affect the outcomes of statistical tests, especially in cases where a large pct of the information are non-detect or zero. Helsel (1990, 2005) describes a variety of tests and approaches that are more robust and sensible in evaluating this character of data.
Plotting lumber changed data
Information technology is relatively promiscuous to plot logarithm-transformed information in spreadsheet programs. When graphing standard deviations or touchstone errors close to a mean, your error bars will be of equal size up above and below the mean if you plot connected lumber report operating theater apply a log scale in a spreadsheet program. However, the error parallel bars will be unequal (several upside and downside standard deviations) if the y axis vertebra is not log changed.
Wherefore geometric mean for calculating fair financial returns makes sense
Opine you invested with $100. Afterward one year your fund said you doubled your money, or had a 100% return along your investment (OR a 2.0 multiplier). In class two, the fund said your assets unrecoverable 50% of their appreciate (a 0.5 multiplier). What was average time period get back for the entire period? If you take the arithmetic stand for of the multipliers (2.0 and 0.5) and subtract 1, you power think your average return is 25%. This is immoral, because the price of your investment funds went from $100 to $200 back to $100. You in fact had a 0% average financial return for the two-year period. You may find IT remarkable that if you calculate geometric mean of 2.0 and 0.5 and subtract 1, you get the make up average annual issue for the entire period, zero. Keep in bear in mind that this is the average annual restitution for the whole period. The geometric mean of 200% and 50% is still 100%.
If you reiterate the in a higher place instance assuming you had $200 in year one, merely the asset crashed to $10 in year 2 (100%, 2.0 multiplier and -95%, 0.05 multiplier respectively for the two values), the arithmetic mean suggests a ludicrous 2.5% yearbook growth, whereas geometric mean calculates a correct 68.38% average annual loss for the two year period ($100 x .3162 x .3162 =$10).
Those transaction with finance refer to this calculation as the "yearly average rate of rejoinder" or "lobed annual growth rate (CAGR)". Biologists use this calculation for quantifying average universe growth rates, which are as wel called the "intrinsic rate of growth" for embryonic phases of universe growth where there are no density myrmecophilous factors controlling populations.
If the asset measure (or universe) in this example declined to zero (100% loss, multiplier=0.0) you cannot calculate geometrical normal (you lost all your money). You should also avoid subbing values because you are approaching a boundary condition (substituting $1 yields a 90% annual loss terminated the ii years; subbing 1 cent yields a 99% average one-year loss based along geometric tight). As a matter of fact, you should avoid victimization this approach whenever declines exceed 90%. Other authors discover problems with the not-natural dispersion of percent data as it approaches zero, and various shift (logistical, arcsine) are applied to these types of data.
Calculating Geometric Substance with Negative Values
Like zero, IT is impossible to calculate Geometric Mean with negative numbers. However, there are several work-arounds for this problem, all of which want that the negative values be converted or transformed to a meaningful positive equivalent value. Most often, this problem arises when it is sought after to calculate the geometric nasty of a percent change in a population or a business enterprise return, which includes negative numbers.
For example, to calculate the geometrical mean of the values +12%, -8%, and +2%, instead calculate the geometric bastardly of their decimal multiplier factor equivalents of 1.12, 0.92, and 1.02, to compute a geometric mean of 1.0167. Subtracting 1 from this value gives the geometric mean of +1.67% as a net rate of population growth (or in financial circles is called the Compound Annual Growth Order-CAGR).
Incidentally, if you do not have a negative percent value in a data set, you should still convert the percent values to the decimal equivalent multiplier. Information technology is important to agnize that when dealing with percent values, the geometric skilled of percent values does not isochronal the pure mathematics mean of the decimal multiplier equivalents.
E.g.:
Pure mathematics mean of [12%, 4%, 2%] does not equal the Nonrepresentational mean of [1.12,1.04,1.02].
4.6% does not equal 5.9%
Calculating Geometric Means with Both Large Negative and Undeniable Numbers Combined
I have received a number of queries, particularly from those analyzing gene block microarray data sets, about how to calculate geometrical means happening information sets that include both selfsame large and very positive numbers. The psychoanalysis of data to evaluate the similarity of gene blocks is a multiplex topic and the statistics of this field is evolving, and you should perform an Internet research to find the current thinking on this subject.
However, in principal, comparing data sets consisting of very epic negative and positive numbers together is an user-friendly affair, and all that is required is to temporarily suspend the negative signs of the data.
Consider, for model, two sets sample information sets as follows:
| A= {-5,-3,-2, 3} and B={-1, 0, 2, 4}
The arithmetic base of data fit A is -1.75, and the arithmetic mean of information set B is +1.25. A simple Student's t-prove (assuming alpha=0.05 and equal sample variances) would suggest these samples are non statistically different from one another.
This approach would be no different than if you were to calculate geometric beggarly in these two data sets:
| A'={-100000, -1000, -100, 1000} and B'={-10,1,100,10000}
If you were to start the negative signs, take the log, then add the minus sign back happening, you could then compare the agency of the A' and B' information sets. As a matter of fact, you might have noticed that information sets A and B are really the log up (base 10) changed data sets A' and B' (after suspending then adding back the negative signs). You might therefore conclude that A' and B' are non statistically different samples exploitation the same t-test.
Incidentally, in a spreadsheet, you can count on the average of the logs of a set of large destructive and positive numbers pool exploitation this array formula (this example is mean 10):
{=AVERAGE(SIGN(rangename)*LOG(ABS(rangename),10))} = -1.75 for A'.
The true geometric mean of the values is premeditated by the regalia formula:
{=SIGN(range)*GEOMEAN(ABS(drift))} = -1778.28 for A'.
Don't type in the curly brackets in the above formulas, type the formula, and so press CTL-SHIFT-Come in.
Of course, like whatsoever other statistical analysis, you have to make a point you have non violated the assumptions of the statistical try out (in this case you must assume the log transformed data is normally diffused, and the sample variances were equal).
Geometric Mean of Sorted Information
A student recently posed this question: How cause you calculate the geometric mean on grouped data? That is to order, when the data exists as a data range and frequency, what recipe do you practice?
As per the discussion above, there are two ways to draw near this problem:
Method 1: (hardest for grouped information): Calculate the cartesian product of all the values in the data set (absolute frequency of to each one middle-point value), then take the nth steady down of the product, with n organism equal to the cumulative absolute frequency.
Method 2: (easiest for grouped information): Calculated the average weighted mean of the log of each middle-point value, then change this base value back to a establish 10 number.
These two statements are best illustrated by the sample data set in the table infra.
| Arithmetic Mean Calculation | Geometric Mean Calculation (Meth. 1) | ||||
| tramp | frequency | midpoint | freq x mid | ln(midpt) | freq x ln(midpt) |
| 10 to >=20 | 3 | 15 | 45 | 2.708 | 8.124 |
| 20 to >=30 | 9 | 25 | 225 | 3.219 | 28.970 |
| 30 to >=40 | 5 | 35 | 175 | 3.555 | 17.777 |
| Total | 17 | 445 | 54.871 | ||
| arithmetic mean= | 26.176 | arithmetic bastardly of weighted ln= | 3.228 | ||
Using Method 1, you would take the 17th root of the production
15 x 15 x 15 x 25 x 25 x 25 x 25 x 25 x 25 x 25 x 25 x 25 x 35 x 35 x 35 x 35 x 35,
which is besides equal to 25.221.
In a spreadsheet, you would type this formula:
=((15^3)*(25^9)*(35^5))^(1/17)
As you might imagine, if you have large middle-point values operating room large frequencies, your estimator or spreadsheet program could not cipher the formula because the intermediate numbers are impossibly large, and the result would be an error. To calculate geometric mean in these cases, you must use Method acting 2. You might also consider the spreadsheet "array formula" method acting in the "Excel #Num! overflow erroneous belief" callout box seat higher up. If your grouped data includes large negative numbers, you wealthy person No choice but regard as a clever transformation to make the values positive and use Method acting 2.
For Method acting 2, as shown in the postpone to a higher place, you would calculate the weighted mean of the natural logarithms of the mid-taper off values, which in this case is 3.228. When the respect is converted support to base 10, the geometric mean is 25.221.
Interestingly, this problem is quite similar to one bald-faced by the Buzzards Bay NEP, in evaluating the extent of oiling from an oil spill. Therein case, the data consisted of an average width and the length of the beach. E.g., 1500 foot. of beach may have had between 0 and 5 fundament-wide banding of oil, 10,000 feet may have been documented to have a band of oil between 5 and 10 ft., etc. The length of beach oiled became the frequency for the interval.
Whether geometric poor is an appropriate metric for evaluating this type of information, operating room whatsoever other data set, always needs to carefully considered.
Working Backward
This following problem was posed by a student:
If Geomean(8,a)=12, what is a?
The doubtfulness can be most easily be rephrased using the nth theme definition of geometric mean. That is:
guileless root of (8 x a)=12
puzzle out first by squaring both sides:
(8xa)=144
a=144/8 = 18
Victimization logs, the mathematical solution is:
Outset give tongue to the problem as the beggarly of logs:
(ln(8)+ln(a))/2 =ln(12)
Resolution:
ln(8)+ln(a) =2 x ln(12) ===> ln(a)=(2 x ln(12))-ln(8) ===>a =exp((2 x ln(12))-ln(8)) ===> a=exp(2.8904) ===> a=18
Exceedances and Too Numerous to Count (TNTC)
In the case of reporting bacteria geometric means, problematic data include non only samples less than the limit of detection, but as wel those samples where settlement forming units (CFUs) are too numerous to reckoning. The upper confine in the number of bacterium colonies that can be counted on an incubation plate depends connected a number of factors that relate to merging of colonies, swarming, and the size of the plate. How these plates are reported depends on method used and coverage protocols. E.g., most agencies that issue discharge permits discourage Oregon prohibit the use of TNTC. Instead they require the reporting of values as "> x." E.g., under ASTM (7), if with a 1:10 dilution, only 200 CFU could be meaningfully counted, the results would reported as >2,000 CFU/ml. In the character of discharge monitoring of under EPA's NPDES program, where unit of time geometric means are reported, the ">" sign is stripped and the economic value used in the geometric mean calculation (e.g. Florida DEP, 2012). In the Food and Drug Administration shellfish sanitation program protocols, "individual plates which are as well numerous to count (TNTC) are well-advised to hold >100 colonies per plate. A sample containing "TNTC" plates is jointly rendered equally having a count of 10,000″ (FDA National Mollusc Sanitation Program Guide for the Control of Molluscan Mollusc 2007 ).
Spreadsheet Tips
If your data contains censored (> and <) information, you could deal using one of these formulas (where the data is in chromatography column c):
If you wanted to convert values by a convinced multiple (half for < data and double for > data in that example), you could use this formula:
=IF(LEFT(C1,1)="<",Note value(Middle(C1,2,20))/2,IF(LEFT(C1,1)=">",VALUE(MID(C1,2,20))*2,C1))
If you wanted to utilise the United States FDA censored data protocol (tapering off or increasing by peerless significant finger's breadth), this complicated pattern should piece of work:
=IF(LEFT(C1,1)="<",VALUE(Middle(C1,2,20))-10^INT(LOG10(ABS(Measure(MID(C1,2,20)))))/10,IF(Left-hand(C1,1)=">",VALUE(MID(C1,2,20))+10^INT(LOG10(ABS(VALUE(MID(C1,2,20)))))/10,C1))
Make sure you clean out any hidden spaces before of the > and < by highlight the column and replacing space with goose egg.
Answer
The response to the psychical math job above: The exponents add up to 20, 20 bilocular by 5 is 4, and so the geometric mean is 24 or 16.
References Cited
EPA 2002, Evolution Document for Projected Sewer water Limitations Guidelines and Standards for the Centered Aquatic Animal Production Industry Point Generator Family. see APPENDIX E: MODIFIED DELTA-LOG NORMAL DISTRIBUTION and APPENDIX F: ALTERNATIVE STATISTICAL METHODS
Dennis R. Helsel. 1990. Fewer THAN OBVIOUS: Applied math Treatment of Data Below the Reporting Specify
Dennis R. Helsel. 2005. More Than Obvious: Better Methods for Interpreting Nondetect Information
Florida DEP. 2012. Subservient Tips For Completing The Sewer water Discharge Monitoring Report (DMR), Sewer water Complaisance Evaluation Subdivision, Bureau of Water Facilities Regulation, February 2012.
Kayhanian, M., Amardeep Singh, and Scott Meyer. "Impact of not-detects in water quality information on idea of constituent mass freight." Weewe Science and Technology 45.9 (2002): 219-225.
McDonald, John H. Vade mecum of biological statistics. Vol. 2. Baltimore, Medic: Sparky House Publication, 2009.
what is the geometric mean of 175 and 7
Source: https://buzzardsbay.org/special-topics/calculating-geometric-mean/



![What to do if your printer prints paper crooked [EXPERT FIX]](http://cdn.windowsreport.com/wp-content/uploads/2019/05/Fix-My-printer-prints-paper-crooked.jpg)
Posting Komentar untuk "what is the geometric mean of 175 and 7"